Workflow: How to use the serosurvey R package?

Context

Problem

  • If we used an imperfect test to measure an outcome within a multi-stage sampling design survey, we need to incorporate the test uncertainty into the sampling design uncertainty.

Method details

survey:

  • Sampling weights were included in a two-stage cluster sample without stratas. We estimated prevalence 95% confidence intervals using the “logit” method.

serology:

  • Here we applied a Bayesian method to estimate the posterior probability of seroprevalence for a test with unknown performance (Daniel B. Larremore et al. 2020).

  • As inputs we used the expanded point estimate number of positive tests and total population that resulted from the sampling weights adjusted seroprevalence estimation.

  • To maintain the sampling design uncertainty, we applied the same method for each estimated confidence interval.

  • Since test sensitivity and specificity were unknown, we used the reported number of true positives, false positives, true negatives and false negatives from a local test performance evaluation.

  • For this worlflow we used lab validation results from an example available in the epiR package: ?epiR::epi.tests

    • for sensitivity: Of 744 patients that were disease positive, 670 were test positive.
    • for specificity: Of 842 patients that were disease negative, 640 were test negative.

Workflow details

  • In this reprex the survey design does not include any explicit strata. Include it if available in I.3.

  • The family of functions serosvy_*_sample_posterior to correct prevalence due to test performance require positive integers. This is adressed in II.2.1.

  • We use purrr and furrr within a for-loop in II.2.2 to efficiently update prevalence posterior distributions for multiple prevalences.

Limitations

  • We do not apply a multiple subpopulation aproach for the inference of prevalence. This is currently available for a test with known performance (Daniel B Larremore et al. 2020).

  • This workflow is only applicable to categorical variables.

  • set.seed could not control the variability generated by test correction functions.

Import packages

# package
library(serosurvey)
# additional
library(tidyverse)
library(srvyr)
library(survey)
library(tictoc)
library(furrr)
library(purrr)
# theme
theme_set(theme_bw())

I. Workflow: Create a survey design object

I.1. Import data

  • datasurvey is the input dataframe
  • outcomes: outcome_one and outcome_two
  • covariates: covariate_01 and covariate_02

I.2. Identify sets numerators and denominators

  • Using select and colnames we create strings of covariates

I.3. Create a srvyr survey design object

I.4 Example: Single estimation

  • How to use serosvy_proportion for a single estimation

  • Here we exchage the numerator and denominator

II. Workflow: Multiple estimation

II.1. Estimates: raw + weighted

outcome_01_pre <- 
  # create a expanded grid of numerators and denominators
  #
  # set 01 of denominator-numerator
  #
  expand_grid(
    design=list(design),
    denominator=covariate_set01, # covariates
    numerator=outcome_set00 # outcomes
  ) %>% 
  #
  # set 02 of denominator-numerator (e.g. within main outcome)
  #
  union_all(
    expand_grid(
      design=list(design),
      denominator=outcome_set00, # outcomes
      numerator=covariate_set02 # covariates
    )
  ) %>% 
  #
  # create symbols (to be readed as arguments)
  #
  mutate(
    denominator=map(denominator,dplyr::sym),
    numerator=map(numerator,dplyr::sym)
  ) %>% 
  #
  # estimate prevalence
  #
  mutate(output=pmap(.l = select(.,design,denominator,numerator),
                     .f = serosvy_proportion)) %>% 
  #
  # show the outcome
  #
  select(-design,-denominator,-numerator) %>% 
  unnest(cols = c(output)) #%>% 

outcome_01_pre
#> # A tibble: 25 x 23
#>    denominator denominator_lev~ numerator numerator_level   prop prop_low
#>    <chr>       <fct>            <chr>     <fct>            <dbl>    <dbl>
#>  1 covariate_~ E                outcome_~ negative        0.211   0.130  
#>  2 covariate_~ E                outcome_~ positive        0.789   0.675  
#>  3 covariate_~ H                outcome_~ negative        0.852   0.564  
#>  4 covariate_~ H                outcome_~ positive        0.148   0.0377 
#>  5 covariate_~ M                outcome_~ negative        0.552   0.224  
#>  6 covariate_~ M                outcome_~ positive        0.448   0.160  
#>  7 covariate_~ E                outcome_~ positive        0.182   0.0499 
#>  8 covariate_~ E                outcome_~ negative        0.818   0.515  
#>  9 covariate_~ H                outcome_~ positive        0.0769  0.00876
#> 10 covariate_~ H                outcome_~ negative        0.923   0.560  
#> # ... with 15 more rows, and 17 more variables: prop_upp <dbl>,
#> #   prop_cv <dbl>, prop_se <dbl>, total <dbl>, total_low <dbl>,
#> #   total_upp <dbl>, total_cv <dbl>, total_se <dbl>, total_deff <dbl>,
#> #   total_den <dbl>, total_den_low <dbl>, total_den_upp <dbl>,
#> #   raw_num <int>, raw_den <int>, raw_prop <dbl>, raw_prop_low <dbl>,
#> #   raw_prop_upp <dbl>

II.2. Add uncertain test performance

II.2.2 Apply to all rows and extract the results

  • Here we use purrr and furrr within a for-loop to efficiently update prevalence posterior distributions for multiple prevalences.

  • We apply the procedure to each point estimate and confidence interval

# 56-60sec por covariable 
# 4GB RAM
# parallelized in 8 cores using purrr y furrr

plan(multisession, workers = availableCores())
tic()

out <- tibble()

for (i in 1:nrow(outcome_01_adj_pre)) {
  
  out <- outcome_01_adj_pre %>% 
    
    slice(i) %>% 
    
    # dot
    mutate(adj_dot_unk=future_pmap(
      .l = select(.,
                  positive_number_test=total_round,
                  total_number_test=total_den_round),
      .f = possibly(serosvy_unknown_sample_posterior,otherwise = NA_real_),
      true_positive = true_positive,
      false_negative = false_negative,
      false_positive = false_positive,
      true_negative = true_negative)) %>% 
    serosvy_extract_posterior(variable = adj_dot_unk) %>% 
    
    # low
    mutate(adj_low_unk=future_pmap(
      .l = select(.,
                  positive_number_test=total_low_round,
                  total_number_test=total_den_low_round),
      .f = possibly(serosvy_unknown_sample_posterior,otherwise = NA_real_),
      true_positive = true_positive,
      false_negative = false_negative,
      false_positive = false_positive,
      true_negative = true_negative)) %>%
    serosvy_extract_posterior(variable = adj_low_unk) %>%
    
    # upp
    mutate(adj_upp_unk=future_pmap(
      .l = select(.,
                  positive_number_test=total_upp_round,
                  total_number_test=total_den_upp_round),
      .f = possibly(serosvy_unknown_sample_posterior,otherwise = NA_real_),
      true_positive = true_positive,
      false_negative = false_negative,
      false_positive = false_positive,
      true_negative = true_negative)) %>%
    serosvy_extract_posterior(variable = adj_upp_unk) %>% 
    
    # union all outputs
    union_all(out)
  
  # activate to print the progress! (recommended)
  # out %>% print() #%>% 
  
  # # known test
    # mutate(adj_dot_kno=future_pmap(
    #   .l = select(.,
    #               positive_number_test=total_round,
    #               total_number_test=total_den_round),
    #   .f = possibly(serosvy_known_sample_posterior,otherwise = NA_real_),
    #   sensitivity=0.999,
    #   specificity=0.960))
  
}

toc()
#> 573.72 sec elapsed

outcome_01_adj <- out  %>% 
  mutate(rowname=as.numeric(rowname)) %>% 
  arrange(rowname) %>% 
  select(-rowname)

II.3. Create output format

  • Here we join all the results to the original dataset

  • We also create unite*_ columns summarizing the results

II.4. Evaluate output

  • Take a quick look to the output:

    • raw_or_unadjusted_prev crude or raw prevalence
    • sampling_weighted_prev sampling weights adjusted prevalence
    • sampling_and_test_prev sampling weights and test performance adjusted prevalence
denominator denominator_level numerator numerator_level raw_num raw_den raw_or_unadjusted_prev sampling_weighted_prev sampling_and_test_prev prop_cv
covariate_01 E outcome_one positive 63 83 75.9 (65.3 - 84.6) 78.9 ( 67.5 - 87) 83.150 (65.89 - 95.5) 0.06
covariate_01 H outcome_one positive 5 20 25.0 ( 8.7 - 49.1) 14.8 ( 3.8 - 44) 0.425 ( 0.28 - 29.9) 0.59
covariate_01 M outcome_one positive 15 23 65.2 (42.7 - 83.6) 44.8 ( 16.0 - 78) 31.506 ( 0.40 - 81.1) 0.38
covariate_01 E outcome_two positive 5 83 6.0 ( 2.0 - 13.5) 18.2 ( 5.0 - 49) NA 0.58
covariate_01 H outcome_two positive 1 20 5.0 ( 0.1 - 24.9) 7.7 ( 0.9 - 44) NA 0.96
covariate_02 Yes outcome_one positive 83 89 93.3 (85.9 - 97.5) 96.7 ( 88.2 - 99) 99.901 (96.99 - 100.0) 0.02
covariate_02 No outcome_two positive 3 37 8.1 ( 1.7 - 21.9) 21.8 ( 6.7 - 52) NA 0.51
covariate_02 Yes outcome_two positive 3 89 3.4 ( 0.7 - 9.5) 9.1 ( 2.1 - 32) NA 0.68
outcome_one positive covariate_02 Yes 83 83 100.0 (95.7 - 100.0) 100.0 (100.0 - 100) NA 0.00
outcome_two positive covariate_02 No 3 6 50.0 (11.8 - 88.2) 54.9 ( 29.4 - 78) NA 0.15
outcome_two positive covariate_02 Yes 3 6 50.0 (11.8 - 88.2) 45.1 ( 21.9 - 71) NA 0.19

II.5. Output figure

  • Make a quick plot using a custom created function

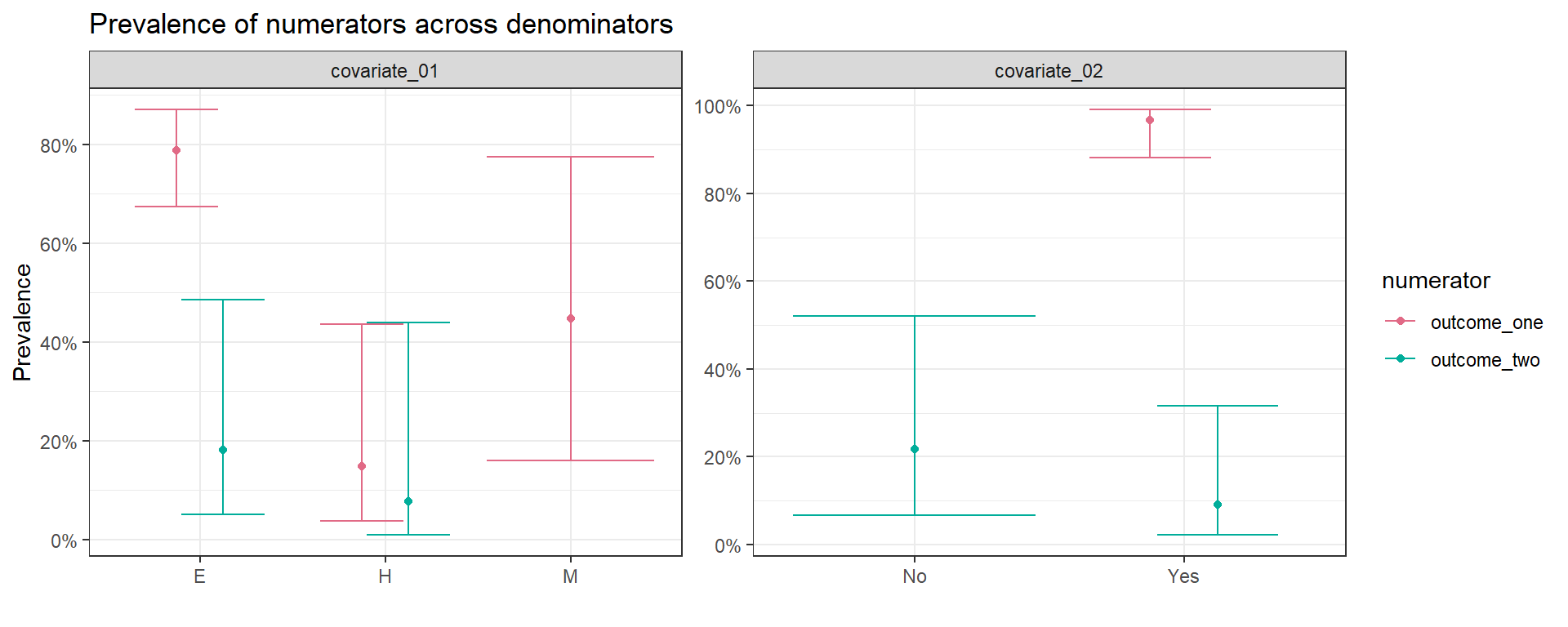
Reference

Larremore, Daniel B, Bailey K Fosdick, Kate M Bubar, Sam Zhang, Stephen M Kissler, C. Jessica E. Metcalf, Caroline Buckee, and Yonatan Grad. 2020. “Estimating SARS-CoV-2 Seroprevalence and Epidemiological Parameters with Uncertainty from Serological Surveys.” medRxiv, April. https://doi.org/10.1101/2020.04.15.20067066.

Larremore, Daniel B., Bailey K. Fosdick, Sam Zhang, and Yonatan H. Grad. 2020. “Jointly Modeling Prevalence, Sensitivity and Specificity for Optimal Sample Allocation.” bioRxiv, May. https://doi.org/10.1101/2020.05.23.112649.