Introduction: serosurvey R package

Introduction

Here we present three examples, definitions and related references:

library(serosurvey)

2. survey: Estimate multiple prevalences

  • In the Article tab we provide a workflow to estimate multiple prevalences:

    • using different set of covariates and outcomes as numerators or denominators,
    • in one single pipe operation
# crear matriz
  #
  # set 01 of denominator-numerator
  #
expand_grid(
  design=list(design),
  denominator=c("covariate_01","covariate_02"), # covariates
  numerator=c("outcome_one","outcome_two") # outcomes
  ) %>% 
  #
  # set 02 of denominator-numerator (e.g. within main outcome)
  #
  union_all(
    expand_grid(
      design=list(design),
      denominator=c("outcome_one","outcome_two"), # outcomes
      numerator=c("covariate_02") # covariates
    )
  ) %>% 
  #
  # create symbols (to be readed as arguments)
  #
  mutate(
    denominator=map(denominator,dplyr::sym),
    numerator=map(numerator,dplyr::sym)
  ) %>% 
  #
  # estimate prevalence
  #
  mutate(output=pmap(.l = select(.,design,denominator,numerator),
                     .f = serosvy_proportion)) %>% 
  #
  # show the outcome
  #
  select(-design,-denominator,-numerator) %>% 
  unnest(cols = c(output)) %>% 
  print(n=Inf)
#> # A tibble: 25 x 23
#>    denominator denominator_lev~ numerator numerator_level   prop prop_low
#>    <chr>       <fct>            <chr>     <fct>            <dbl>    <dbl>
#>  1 covariate_~ E                outcome_~ No              0.211   0.130  
#>  2 covariate_~ E                outcome_~ Yes             0.789   0.675  
#>  3 covariate_~ H                outcome_~ No              0.852   0.564  
#>  4 covariate_~ H                outcome_~ Yes             0.148   0.0377 
#>  5 covariate_~ M                outcome_~ No              0.552   0.224  
#>  6 covariate_~ M                outcome_~ Yes             0.448   0.160  
#>  7 covariate_~ E                outcome_~ (-0.1,50]       0.182   0.0499 
#>  8 covariate_~ E                outcome_~ (50,100]        0.818   0.515  
#>  9 covariate_~ H                outcome_~ (-0.1,50]       0.0769  0.00876
#> 10 covariate_~ H                outcome_~ (50,100]        0.923   0.560  
#> 11 covariate_~ M                outcome_~ (50,100]        1.00    1.00   
#> 12 covariate_~ No               outcome_~ No              1.00    1.00   
#> 13 covariate_~ Yes              outcome_~ No              0.0334  0.00884
#> 14 covariate_~ Yes              outcome_~ Yes             0.967   0.882  
#> 15 covariate_~ No               outcome_~ (-0.1,50]       0.218   0.0670 
#> 16 covariate_~ No               outcome_~ (50,100]        0.782   0.479  
#> 17 covariate_~ Yes              outcome_~ (-0.1,50]       0.0914  0.0214 
#> 18 covariate_~ Yes              outcome_~ (50,100]        0.909   0.684  
#> 19 outcome_one No               covariat~ No              0.939   0.778  
#> 20 outcome_one No               covariat~ Yes             0.0615  0.0148 
#> 21 outcome_one Yes              covariat~ Yes             1.00    1.00   
#> 22 outcome_two (-0.1,50]        covariat~ No              0.549   0.294  
#> 23 outcome_two (-0.1,50]        covariat~ Yes             0.451   0.219  
#> 24 outcome_two (50,100]         covariat~ No              0.305   0.188  
#> 25 outcome_two (50,100]         covariat~ Yes             0.695   0.546  
#> # ... with 17 more variables: prop_upp <dbl>, prop_cv <dbl>,
#> #   prop_se <dbl>, total <dbl>, total_low <dbl>, total_upp <dbl>,
#> #   total_cv <dbl>, total_se <dbl>, total_deff <dbl>, total_den <dbl>,
#> #   total_den_low <dbl>, total_den_upp <dbl>, raw_num <int>,
#> #   raw_den <int>, raw_prop <dbl>, raw_prop_low <dbl>, raw_prop_upp <dbl>

learnr tutorial

  • Learn to build this with in a tutorial in Spanish:
# install learner and run tutorial
if(!require("learnr")) install.packages("learnr")
learnr::run_tutorial(name = "taller",package = "serosurvey")

3. serology: Estimate prevalence Under misclassification

  • We gather one frequentist approach (Rogan and Gladen 1978), available in different Github repos, that deal with misclassification due to an imperfect diagnostic test (Azman et al. 2020; Takahashi, Greenhouse, and Rodríguez-Barraquer 2020). Check the Reference tab.

  • We provide tidy outputs for bayesian approaches developed in Daniel B. Larremore et al. (2020) here and Daniel B Larremore et al. (2020) here:

  • You can use them with purrr and furrr to efficiently iterate and parallelize this step for multiple prevalences. Check the workflow in Article tab.

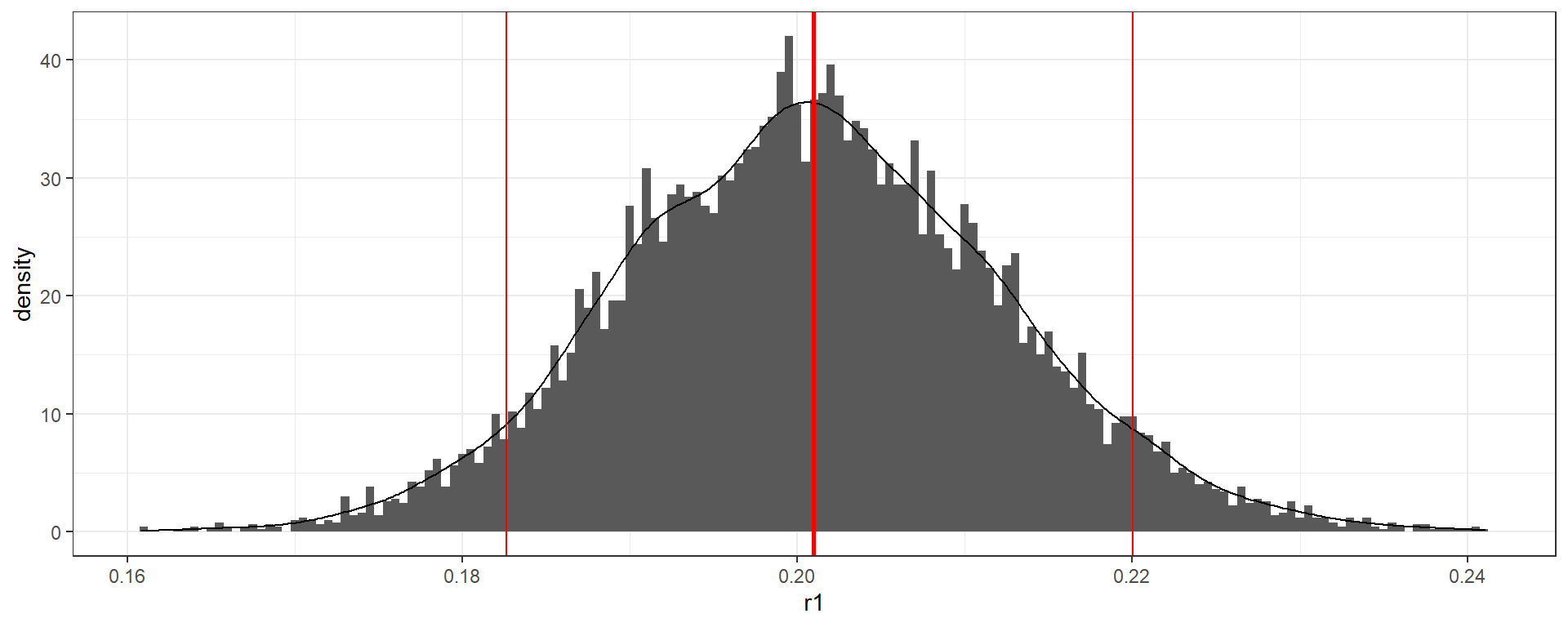
Known test performance - Bayesian method 

example("serosvy_known_sample_posterior")

Unknown test performance - Bayesian method

  • The test performance is called “unknown” or “uncertain” when test sensitivity and specificity are not known with certainty (Kritsotakis 2020; Diggle 2011; Gelman and Carpenter 2020) and lab validation data is available with a limited set of samples, tipically during a novel pathogen outbreak.

example("serosvy_unknown_sample_posterior")

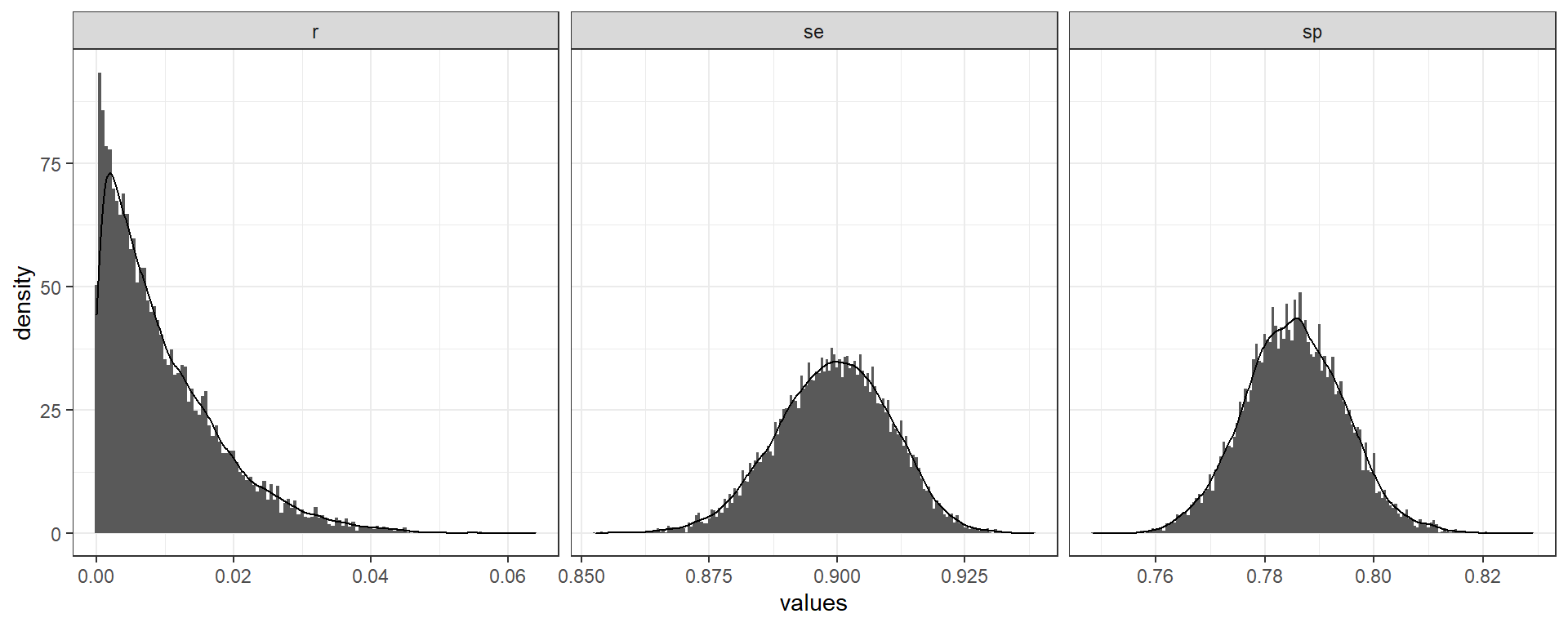
Contributing

Feel free to fill an issue or contribute with your functions or workflows in a pull request.

Here are a list of publications with interesting approaches using R:

  • Silveira et al. (2020) and Hallal et al. (2020) analysed a serological survey accounting for sampling design and test validity using parametric bootstraping, following Lewis and Torgerson (2012).

  • Flor et al. (2020) implemented a lot of frequentist and bayesian methods for test with known sensitivity and specificity. Code is available here.

  • Gelman and Carpenter (2020) also applied Bayesian inference with hierarchical regression and post-stratification to account for test uncertainty with unknown specificity and sensitivity. Here a case-study.

References

Azman, Andrew S, Stephen Lauer, M. Taufiqur Rahman Bhuiyan, Francisco J Luquero, Daniel T Leung, Sonia Hegde, Jason B Harris, et al. 2020. “Vibrio Cholerae O1 Transmission in Bangladesh: Insights from a Nationally- Representative Serosurvey,” March. https://doi.org/10.1101/2020.03.13.20035352.

Diggle, Peter J. 2011. “Estimating Prevalence Using an Imperfect Test.” Epidemiology Research International 2011: 1–5. https://doi.org/10.1155/2011/608719.

Flor, Matthias, Michael Weiß, Thomas Selhorst, Christine Müller-Graf, and Matthias Greiner. 2020. “Comparison of Bayesian and Frequentist Methods for Prevalence Estimation Under Misclassification.” BMC Public Health 20 (1). https://doi.org/10.1186/s12889-020-09177-4.

Gelman, Andrew, and Bob Carpenter. 2020. “Bayesian Analysis of Tests with Unknown Specificity and Sensitivity.” Journal of the Royal Statistical Society: Series C (Applied Statistics), August. https://doi.org/10.1111/rssc.12435.

Hallal, Pedro C, Fernando P Hartwig, Bernardo L Horta, Mariângela F Silveira, Claudio J Struchiner, Luı́s P Vidaletti, Nelson A Neumann, et al. 2020. “SARS-CoV-2 Antibody Prevalence in Brazil: Results from Two Successive Nationwide Serological Household Surveys.” The Lancet Global Health, September. https://doi.org/10.1016/s2214-109x(20)30387-9.

Kritsotakis, Evangelos I. 2020. “On the Importance of Population-Based Serological Surveys of SARS-CoV-2 Without Overlooking Their Inherent Uncertainties.” Public Health in Practice 1 (November): 100013. https://doi.org/10.1016/j.puhip.2020.100013.

Larremore, Daniel B, Bailey K Fosdick, Kate M Bubar, Sam Zhang, Stephen M Kissler, C. Jessica E. Metcalf, Caroline Buckee, and Yonatan Grad. 2020. “Estimating SARS-CoV-2 Seroprevalence and Epidemiological Parameters with Uncertainty from Serological Surveys.” medRxiv, April. https://doi.org/10.1101/2020.04.15.20067066.

Larremore, Daniel B., Bailey K. Fosdick, Sam Zhang, and Yonatan H. Grad. 2020. “Jointly Modeling Prevalence, Sensitivity and Specificity for Optimal Sample Allocation.” bioRxiv, May. https://doi.org/10.1101/2020.05.23.112649.

Lewis, Fraser I, and Paul R Torgerson. 2012. “A Tutorial in Estimating the Prevalence of Disease in Humans and Animals in the Absence of a Gold Standard Diagnostic.” Emerging Themes in Epidemiology 9 (1). https://doi.org/10.1186/1742-7622-9-9.

Rogan, Walter J., and Beth Gladen. 1978. “Estimating Prevalence from the Results of A Screening Test.” American Journal of Epidemiology 107 (1): 71–76. https://doi.org/10.1093/oxfordjournals.aje.a112510.

Silveira, Mariângela F., Aluı́sio J. D. Barros, Bernardo L. Horta, Lúcia C. Pellanda, Gabriel D. Victora, Odir A. Dellagostin, Claudio J. Struchiner, et al. 2020. “Population-Based Surveys of Antibodies Against SARS-CoV-2 in Southern Brazil.” Nature Medicine 26 (8): 1196–9. https://doi.org/10.1038/s41591-020-0992-3.

Takahashi, Saki, Bryan Greenhouse, and Isabel Rodríguez-Barraquer. 2020. “Are SARS-CoV-2 seroprevalence estimates biased?” The Journal of Infectious Diseases, August. https://doi.org/10.1093/infdis/jiaa523.